Introducción a las Redes Neuronales Parte 1 - Regresión Binaria

• 1. Introducción
• 2. Regresión Binaria
• 3. Entrenamiento y Entropía
  • 3.1 Función de pérdida (Entropía cruzada)
• 4. Ejemplo práctico en Python
• 5. Regresión Multinomial
• 6. Conclusión
• Referencias

1. Introducción

El objetivo de esta serie de posts, de Introducción a las Redes Neuronales, es dar unas pinceladas a qué es una red neuronal, y por qué está dando tanto que hablar en los últimos años.

En esta primera parte, introduciremos un concepto básico para poder entender las redes neuronales, los denominados regresores, su intuición matemática, y construiremos algún ejemplo en Python usando numpy y pytorch.

2. Regresión Binaria

El objetivo de la regresión binaria o logística es entrenar un clasificador que sea capaz de distinguir entre dos clases, a partir de nuevas entradas; y construir lo que denominamos la frontera de decisión (decision boundary). Es decir, queremos saber la probabilidad de que dada una entrada $x$, la salida $y$ que obtengamos sea 1, $P(y=1|x)$.

La regresión logística resuelve este problema aprendiendo a partir de un conjunto de datos, que denominaremos de entrenamiento, un vector de pesos $w$ y un sesgo $b$. Cada peso $w_i$ es un número real asociada a cada una de las características (features) o columnas de entradas $x_i$.

$$z=(\sum _{i=1}^n{w}_i{x}_i)+b$$

El cómo aprende estos pesos lo veremos en el apartado 3.

Para entender su intuición matemática, deberemos recordar que cualquier función lineal puede expresarse mediante la fórmula: $y=mx+b$; donde $m$ es la pendiente y $b$ el punto que pasa por el origen.

Figura 1: Función lineal de Magister Mathematicae - Trabajo propio, CC BY-SA 4.0, https://commons.wikimedia.org/w/index.php?curid=34887966

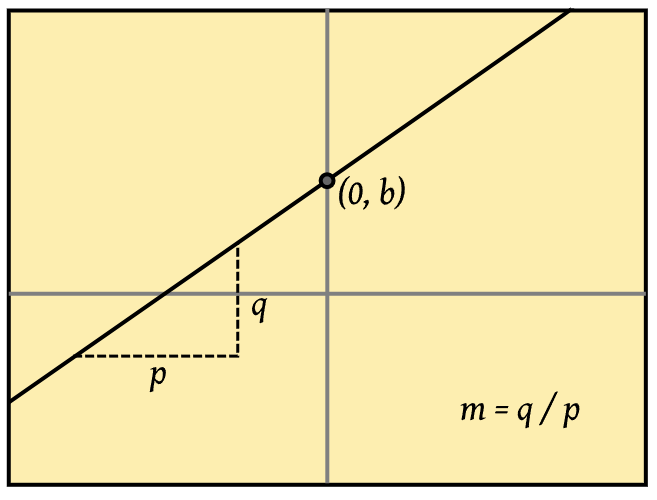
Aquí el sumatorio hace referencia a que la operación $wx$ se trata del producto escalar de ambos vectores, es decir, la suma de los productos componente a componente.

Sin embargo, con esto no es suficiente, y es que esta función toma valores en el rango $(-\mathrm{\infty },\mathrm{\infty })$, y para poder hacerla una probabilidad, necesitamos pasar $z$ a través de la función sigmoide (o logística):

$$\sigma (z)=\frac{1}{1+e^{-z}}$$

Esta función lo que hace es mapear un valor real al rango $[0,1]$, y además es diferenciable, que como veremos más adelante, es algo deseable.

Sólo nos falta un ingrediente para construir el regresor logístico, necesitamos que para que sea realmente una probabilidad, tenemos que asegurarnos que los dos casos, $p(y=1)$ y $p(y=0)$, sumen 1:

$$P(y=1)=1-P(y=0)$$

Decimos que una entrada pertenece a una clase si la probabilidad de pertenecer a esa clase $P(y=1|x)$ es mayor de $0.5$, y que no pertenece a la clase en otro caso. En este caso, $0.5$ es la frontera de decisión.

3. Entrenamiento y Entropía

Llegados a este punto, te estarás preguntando, ¿cómo es que el modelo es capaz de aprender estos valores de $w$ y $b$ por sí solo?

Regresión logística es un modelo de aprendizaje supervisado, en el que conocemos la respuesta correcta $y_i$ (1 o 0) para cada observación $x_i$.

El objetivo es aprender los parámetros $w$ y $b$ para obtener $\hat{y}$ (predicción) lo más cercana al valor verdadero $y$. Para hacerlo posible necesitamos:

• Una función de pérdida, que nos diga cómo de cerca o lejos está nuestra observación del valor real.
• Un algoritmo de optimización, el cual de manera iterativa, actualice los valores de los parámetros para minimizar esta función de pérdida. El algoritmo estándar para esto es el denominado descenso por gradiente estocástico o SGD (por sus siglas en inglés).

Sin entrar en mucho detalle para el algoritmo de optimización, ya que merece una entrada aparte, digamos que es un método que nos permite dada una función de error o coste, con una entrada $w$, encontrar el punto en el que se minimiza la función, es decir, donde el error (diferencia entre $y$ e $\hat{y}$) es mínimo.

Figura 2: Algoritmo de optimización

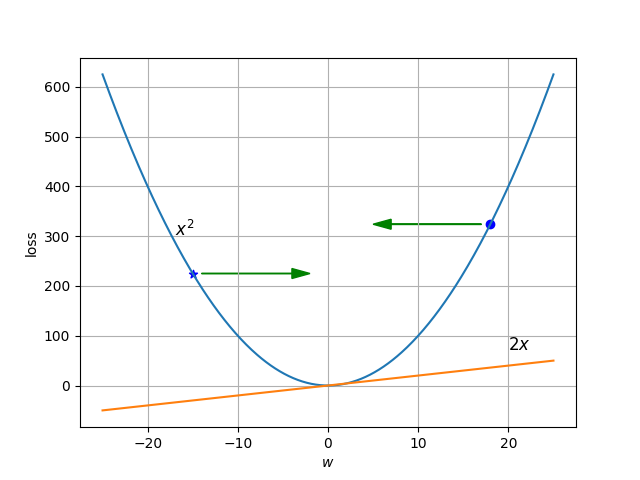
3.1 Función de pérdida (Entropía cruzada)

Vamos a deducir esta función de pérdida por nosotros mismos, para entender la lógica detrás.

Queremos una función que nos dé una puntuación de cómo de parecidos son la observación dada y el valor real, y a esta función la denominamos “estimación de máxima versolimilitud condicional” o conditional maximum likelihood estimation en inglés.

Aplicado a una única observación, queremos aprender los pesos que maximicen la probabilidad de acertar con la predicción $p(y|x)$. Dado que hay únicamente dos posibles casos (1 o 0), esto se traduce en una distribución de Bernoulli:

$$p(y|x)={\hat{y}}^y(1-\hat{y}{)}^{(1-y)}$$

Ahora tomamos logaritmos a ambos lados de la ecuación, ya que facilita los cálculos y mejora el aprendizaje de la red neuronal (castigando fuertemente cuando se producen predicciones erróneneas con valores cercanos a 0):

$$\log p(y|x)=\log [{\hat{y}}^y(1-\hat{y}{)}^{(1-y)}]=y\log \hat{y}+(1-y)\log (1-\hat{y})$$

Y finalmente, queremos convertir el problema en uno de minimización, ya que queremos aquél valor que nos dé el error más pequeño, por tanto, le cambiamos el signo a la función. El resultado es la función de pérdida de entropía cruzada $L_{CE}$:

$$L_{CE}=-\log p(y|x)=-[y\log \hat{y}+(1-y)\log (1-\hat{y})]$$

Por poner un ejemplo, supongamos que estamos clasificando si una imagen contiene un perro $(y=1)$ o no $(y=0)$.

Caso correcto
Si la red predice correctamente que hay un perro con alta confianza ($\hat{y}=0.9$): $L_{CE}=-[1\log 0.9+(1-1)\log (1-0.9)]=-\log 0.9=0.105$

La pérdida es pequeña, lo que indica que la predicción es buena.

Caso incorrecto
Si la red se equivoca y dice que la probabilidad de que haya un perro es baja ($\hat{y}=0.1$): $L_{CE}=-\log 0.1=2.3$

La pérdida es mayor, lo que indica que la red está cometiendo un error grande y necesita ajustar los pesos.

4. Ejemplo práctico en Python

Enhorabuena, ya eres todo un experto en regresores logísticos, así que por qué no bajamos a tierra y ponemos todo esto en práctica.

Para este ejemplo en Python, vamos a crear un regresor logístico sencillo que sea capaz de aprender a diferenciar entre dos clases (0 o 1), dado una entrada $x$. Usando todos los conceptos vistos más arriba.

Figura 3: Visualización de la frontera de decisión

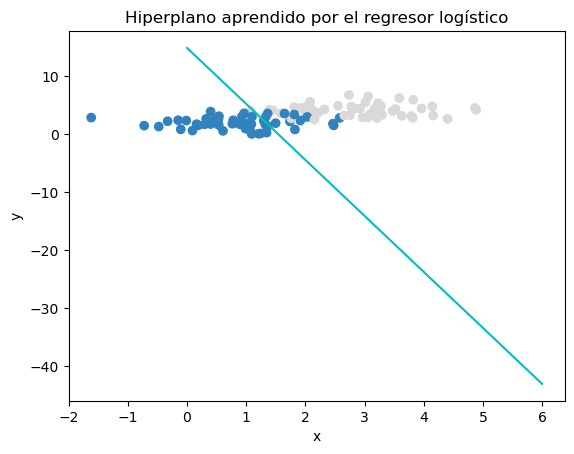
Se asume cierto conocimiento de Python y la librería pytorch para este ejemplo, aunque si estás muy verde en esto, no pasa nada, el notebook contiene anotaciones en texto para que puedas seguir la lógica del mismo.

Algo que no hemos mencionado en los conceptos de arriba, es que en la práctica, aunque se puede hacer, se suelen evitar los bucles para realizar los cálculos, en su lugar, se empaquetan las operaciones en vectores y matrices que se lanzan de una vez para aprovechar el poder de paralelismo de las GPUs. En este ejemplo sencillo, no vamos a notar diferencia alguna, pero cuando vayamos a utilizar datasets de cientos de miles de registros, y matrices de pesos de miles de parámetros, será algo indispensable.

Puedes encontrar el notebook del ejemplo aquí: Open In Colab

5. Regresión Multinomial

Como punto extra, vamos a explicar qué pasa cuando queremos hacer regresión sobre más de dos clases. En este caso, utilizamos la regresión logística multinomial, también llamada regresión softmax.

La regresión multinomial utiliza otra función denominada softmax, la cual toma un vector $z=[z_1,z_2,\dots ,z_K]$ de K posibles clases, y le asigna a cada elemento un valor entre 0 y 1, dando como resultado un vector cuya suma de sus elementos da siempre 1.

$$softmax(z_i)=\frac{exp(z_i)}{\sum _{j=1}^{K}exp(z_j)}$$

La salida $y$ para cada entrada $x$ será un vector de longitud $K$ (número de clases), donde si $c$ es la clase correcta, pondremos en el elemento $y_c=1$, y cero para el resto (one-hot vector).

6. Conclusión

Para finalizar, espero que hayas podido comprender los fundamentos de la regresión logística, desde su intuición matemática hasta su implementación, y sobretodo, que te haya servido para empezar a ver cómo funcionan las redes neuronales en su versión más básica, y en la que seguiremos explorando en próximas entradas.

Referencias

1. Jurafsky, D. and Martin J. (2021). Speech and Language Processing. Chapter 5

2. Perez, J. A. Regresores: conociendo al hermano pequeño de las redes neuronales. Disponible en: https://www.dlsi.ua.es/~japerez/materials/transformers/regresor/

3. Tsuranava, N. (2024) Estudio de la arquitectura neuronal transformer y comparación entre el mecanismo de atención multicabezal frente al multiconsulta. Disponible en: https://rua.ua.es/dspace/bitstream/10045/145624/1/Estudio_de_la_arquitectura_neuronal_transformer_y_compar_Tsuranava__Natallia.pdf